18. Sequences

In general, the process of finding the limit of a sequence is essentially the same as finding the limit at infinity of a continuous function (i.e. finding its horizontal asymptote).

b3. Special Limits

Before discussing the computation of limits of sequences in general, we first present some Special Limits. The Special Limit are intuitively obvious, but the proof links go to the proofs which are at the end of this chapter after the precise definition of the limit of a sequence.

The simplest two sequences are the identity sequence, \(a_n=n\), and the constant sequences, \(a_n=c\) for any number \(c\). Their plots are:

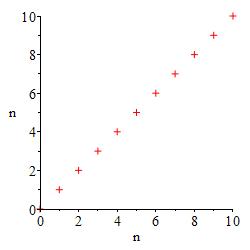
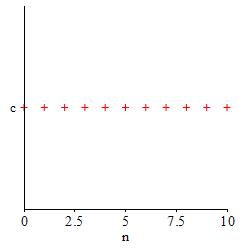
Their limits are given by:

\[ (1) \qquad \lim_{n\to\infty}n=\infty \] Proof

For any number \(c\), \[ (2) \qquad \lim_{n\to\infty}c=c \] Proof

The next two groups of sequences are the power sequences, \(a_n=n^p\), (with a constant power, \(p\)) and the exponential sequences, \(a_n=b^n\), (with a constant base, \(b\)).

If \(p>0\), then \[ (3a) \qquad \lim_{n\to\infty}n^p=\infty \qquad \text{and} \qquad (3b) \qquad \lim_{n\to\infty}\dfrac{1}{n^p}=0. \] If \(p<0\), then \[ (3c) \qquad \lim_{n\to\infty}n^p=0 \qquad \text{and} \qquad (3d) \qquad \lim_{n\to\infty}\dfrac{1}{n^p}=\infty. \] Proof

As examples we have: \[\begin{array}{ll} \lim\limits_{n\to\infty}n^2 =\lim\limits_{n\to\infty}\dfrac{1}{n^{-2}}=\infty \qquad & \lim\limits_{n\to\infty}n^{1/2} =\lim\limits_{n\to\infty}\dfrac{1}{n^{-1/2}} =\lim\limits_{n\to\infty}\sqrt{n}=\infty \\ \lim\limits_{n\to\infty}n^{-2} =\lim\limits_{n\to\infty}\dfrac{1}{n^2}=0 \qquad & \lim\limits_{n\to\infty}n^{-1/2} =\lim\limits_{n\to\infty}\dfrac{1}{n^{1/2}} =\lim\limits_{n\to\infty}\dfrac{1}{\sqrt{n}}=0 \end{array}\] To justify these, try plugging in \(n=1\) million, i.e. \(n=1,000,000=10^6\).

If \(b>1\), then \[ (4a) \qquad \lim_{n\to\infty}b^n=\infty \qquad \text{and} \qquad (4b) \qquad \lim_{n\to\infty}\dfrac{1}{b^n}=0. \] If \(0 < b < 1\), then \[ (4c) \qquad \lim_{n\to\infty}b^n=0 \qquad \text{and} \qquad (4d) \qquad \lim_{n\to\infty}\dfrac{1}{b^n}=\infty. \] Proof

As examples we have: \[\begin{array}{ll} \lim\limits_{n\to\infty}2^n=\infty \qquad &\lim\limits_{n\to\infty}\left(\dfrac{1}{2}\right)^n =\lim\limits_{n\to\infty}\dfrac{1}{2^n}=0 \end{array}\] To justify these, try plugging in \(n=10\) or \(n=20\).

Study the difference between the power and the exponential sequences. The first is the limit of the variable base \(n\) to a fixed power \(p\). The second is the limit of a fixed base \(b\) to the variable power \(n\).